Chapter 3 Complex ANOVA and Multiple Linear Regression

In the One-Way ANOVA and simple linear regression models, there was only one variable - categorical for ANOVA and continuous for simple linear regression - to explain and predict our target variable. Rarely do we believe that only a single variable will suffice in predicting a variable of interest. Here in this Chapter we will generalize these models to the \(n\)-Way ANOVA and multiple linear regression models. These models contain multiple sets of variables to explain and predict our target variable.

This Chapter aims to answer the following questions:

  • How do we include multiple variables in ANOVA?
    • Exploration
    • Assumptions
    • Predictions
  • What is an interaction between two predictor variables?
    • Interpretation
    • Evaluation
    • Within Category Effects
  • What is blocking in ANOVA?
    • Nuisance Factors
    • Differences Between Blocking and Two-Way ANOVA
  • How do we include multiple variables in regression?
    • Model Structure
    • Global & Local Inference
    • Assumptions
    • Adjusted \(R^2\)
    • Categorical Variables in Regression

3.1 Two-Way ANOVA

In the One-Way ANOVA model, we used a single categorical predictor variable with \(k\) levels to predict our continuous target variable. Now we will generalize this model to include \(n\) categorical variables that each have different numbers of levels (\(k_1, k_2, ..., k_n\)).

3.1.1 Exploration

Let’s use the basic example of two categorical predictor variables in a Two-Way ANOVA. Previously, we talked about using heating quality as a factor to explain and predict sale price of homes in Ames, Iowa. Now, we also consider whether the home has central air. Although similar in nature, these two factors potentially provide important, unique pieces of information about the home. Similar to previous data science problems, let us first explore our variables and their potential relationships.

Now that we have two variables that we will use to explain and predict sale price, here are some summary statistics (mean, standard deviation, minimum, and maximum) for each combination of category. We will use the group_by function on both predictor variables of interest to split the data and then the summarise function to calculate the metrics we are interested in.

train %>% 
  group_by(Heating_QC, Central_Air) %>%
  dplyr::summarise(mean = mean(Sale_Price), 
            sd = sd(Sale_Price), 
            max = max(Sale_Price), 
            min = min(Sale_Price),
            n = n())
## `summarise()` has grouped output by 'Heating_QC'. You can override using the
## `.groups` argument.
## # A tibble: 10 × 7
## # Groups:   Heating_QC [5]
##    Heating_QC Central_Air    mean     sd    max    min     n
##    <ord>      <fct>         <dbl>  <dbl>  <int>  <int> <int>
##  1 Poor       N            50050  52255.  87000  13100     2
##  2 Poor       Y           107000     NA  107000 107000     1
##  3 Fair       N            84748. 28267. 158000  37900    29
##  4 Fair       Y           145165. 38624. 230000  50000    36
##  5 Typical    N           103469. 34663. 209500  12789    82
##  6 Typical    Y           142003. 39657. 375000  60000   527
##  7 Good       N           110811. 38455. 214500  59000    23
##  8 Good       Y           160113. 54158. 415000  52000   318
##  9 Excellent  N           115062. 33271. 184900  64000    11
## 10 Excellent  Y           216401. 88518. 745000  58500  1022

We can already see above that there appears to be some differences in average sale price across the categories overall. Within each grouping of heating quality, homes with central air appear to have a higher sale price than homes without. Also, similar to before, homes with higher heating quality appear to have higher sale prices compared to homes with lower heating quality. Careful about samepl size in these situations though!

We also see these relationships in the bar chart in Figure 3.1.

CA_heat <- train %>% 
  group_by(Heating_QC, Central_Air) %>%
  dplyr::summarise(mean = mean(Sale_Price), 
            sd = sd(Sale_Price), 
            max = max(Sale_Price), 
            min = min(Sale_Price), 
            n = n())
## `summarise()` has grouped output by 'Heating_QC'. You can override using the
## `.groups` argument.
ggplot(data = CA_heat, aes(x = Heating_QC, y = mean/1000, fill = Central_Air)) +
  geom_bar(stat = "identity", position = position_dodge()) +
  labs(y = "Sales Price (Thousands $)", x = "Heating Quality Category") +
  scale_fill_brewer(palette = "Paired") +
  theme_minimal()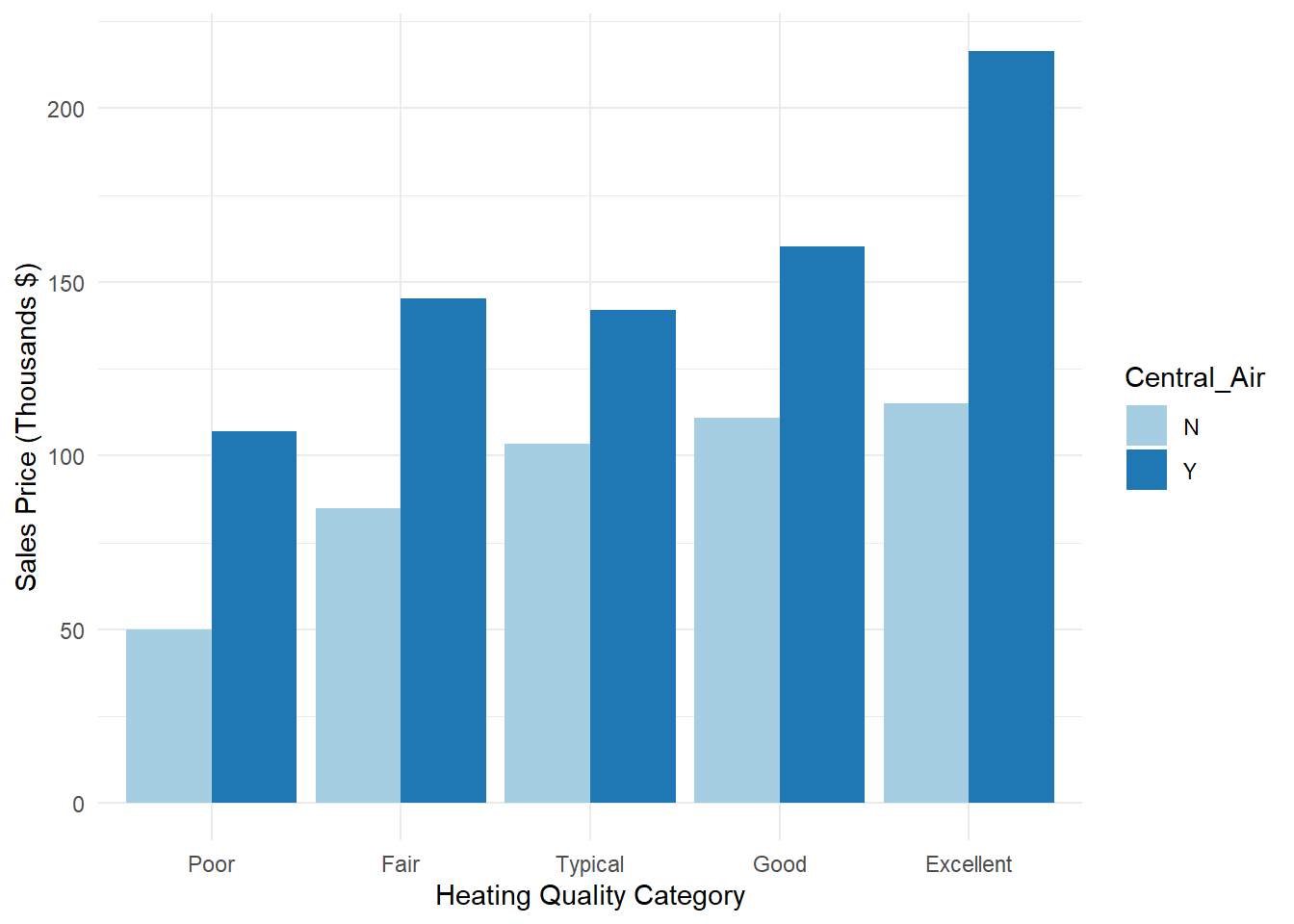
Distribution of Variables Heating_QC and Central_Air

Figure 3.1: Distribution of Variables Heating_QC and Central_Air

As before, visually looking at bar charts and mean calculations only goes so far. We need to statistically be sure of any differences that exist between average sale price in categories.

3.1.2 Model

We are going to do this with the same approach as in the One-Way ANOVA, just with more variables as shown in the following equation:

\[ Y_{ijk} = \mu + \alpha_i + \beta_j + \varepsilon_{ijk} \] where \(\mu\) is the average baseline sales price of a home in Ames, Iowa, \(\alpha_i\) is the variable representing the impacts of the levels of heating quality, and \(\beta_j\) is the variable representing the impacts of the levels of central air. As mentioned previously, the unexplained error in this model is represented as \(\varepsilon_{ijk}\).

The same F test approach is also used, just for each one of the variables. Each variable’s test has a null hypothesis assuming all categories have the same mean. The alternative for each test is that at least one category’s mean is different.

Let’s view the results of the aov function.

ames_aov2 <- aov(Sale_Price ~ Heating_QC + Central_Air, data = train)

summary(ames_aov2)
##               Df    Sum Sq   Mean Sq F value   Pr(>F)    
## Heating_QC     4 2.891e+12 7.228e+11  147.60  < 2e-16 ***
## Central_Air    1 2.903e+11 2.903e+11   59.28 2.11e-14 ***
## Residuals   2045 1.002e+13 4.897e+09                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

From the above results, we have low p-values for each of the variables’ F test. Heating quality had 4 degrees of freedom, derived from the 5 categories \((4 = 5-1)\). Similarly, central air’s 2 categories produce 1 \((= 2-1)\) degree of freedom. The F values are calculated the exact same way as described before with the mean square for each variable divided by the mean square error. Based on these tests, at least one category in each variable is statistically different than the rest.

3.1.3 Post-Hoc Testing

As with the One-Way ANOVA, the next logical question is which of these categories is different. We will use the same post-hoc tests as before with the TukeyHSD function.

tukey.ames2 <- TukeyHSD(ames_aov2)
print(tukey.ames2)
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = Sale_Price ~ Heating_QC + Central_Air, data = train)
## 
## $Heating_QC
##                        diff        lwr       upr     p adj
## Fair-Poor          49176.42 -63650.448 162003.29 0.7571980
## Typical-Poor       67781.01 -42800.320 178362.35 0.4506761
## Good-Poor          87753.89 -23040.253 198548.03 0.1945181
## Excellent-Poor    146288.89  35818.859 256758.92 0.0028361
## Typical-Fair       18604.59  -6326.425  43535.61 0.2484556
## Good-Fair          38577.47  12718.894  64436.04 0.0004622
## Excellent-Fair     97112.47  72679.867 121545.07 0.0000000
## Good-Typical       19972.87   7050.230  32895.52 0.0002470
## Excellent-Typical  78507.88  68746.678  88269.07 0.0000000
## Excellent-Good     58535.00  46602.229  70467.78 0.0000000
## 
## $Central_Air
##         diff      lwr      upr p adj
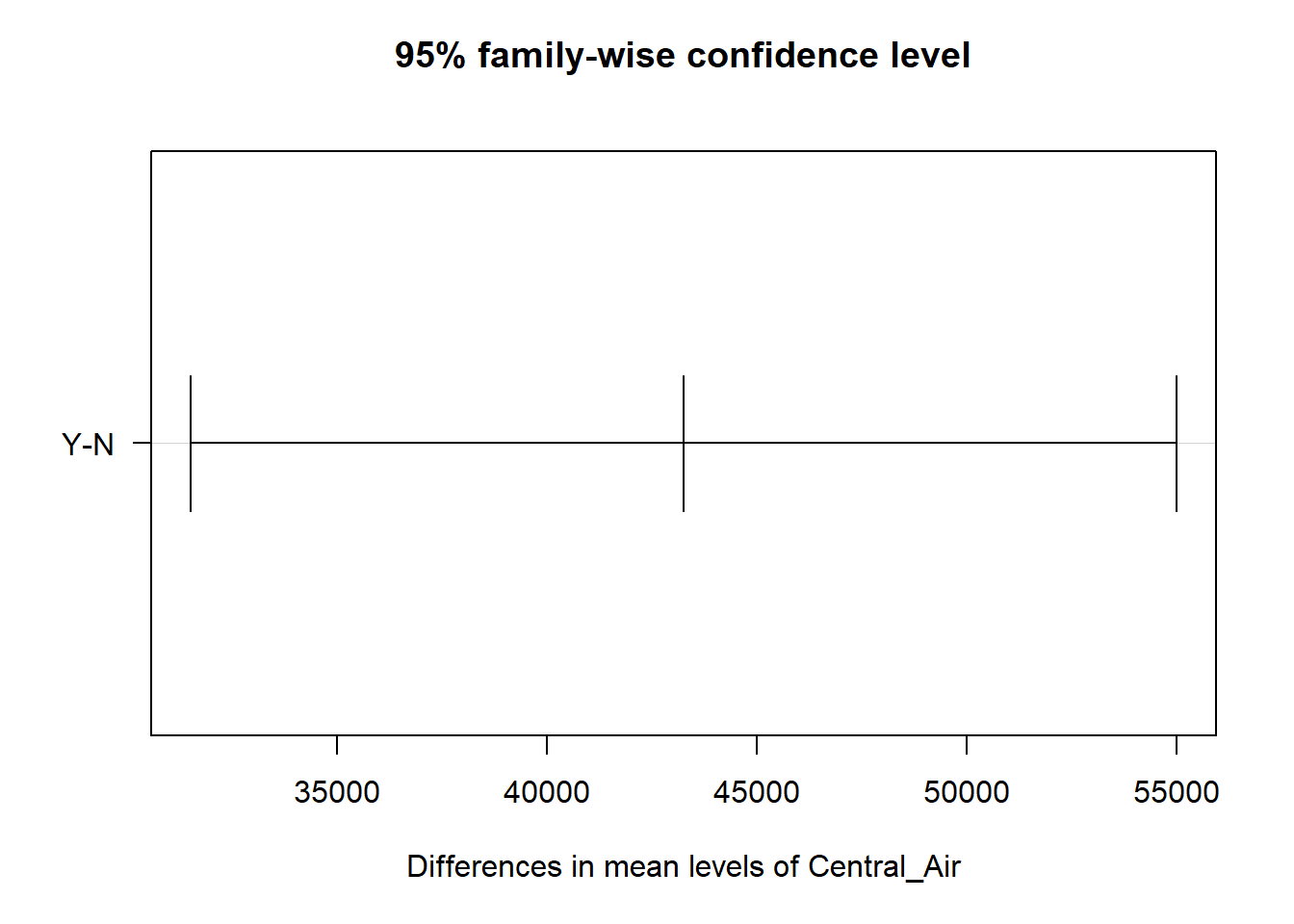
## Y-N 43256.57 31508.27 55004.87     0
plot(tukey.ames2, las = 1)

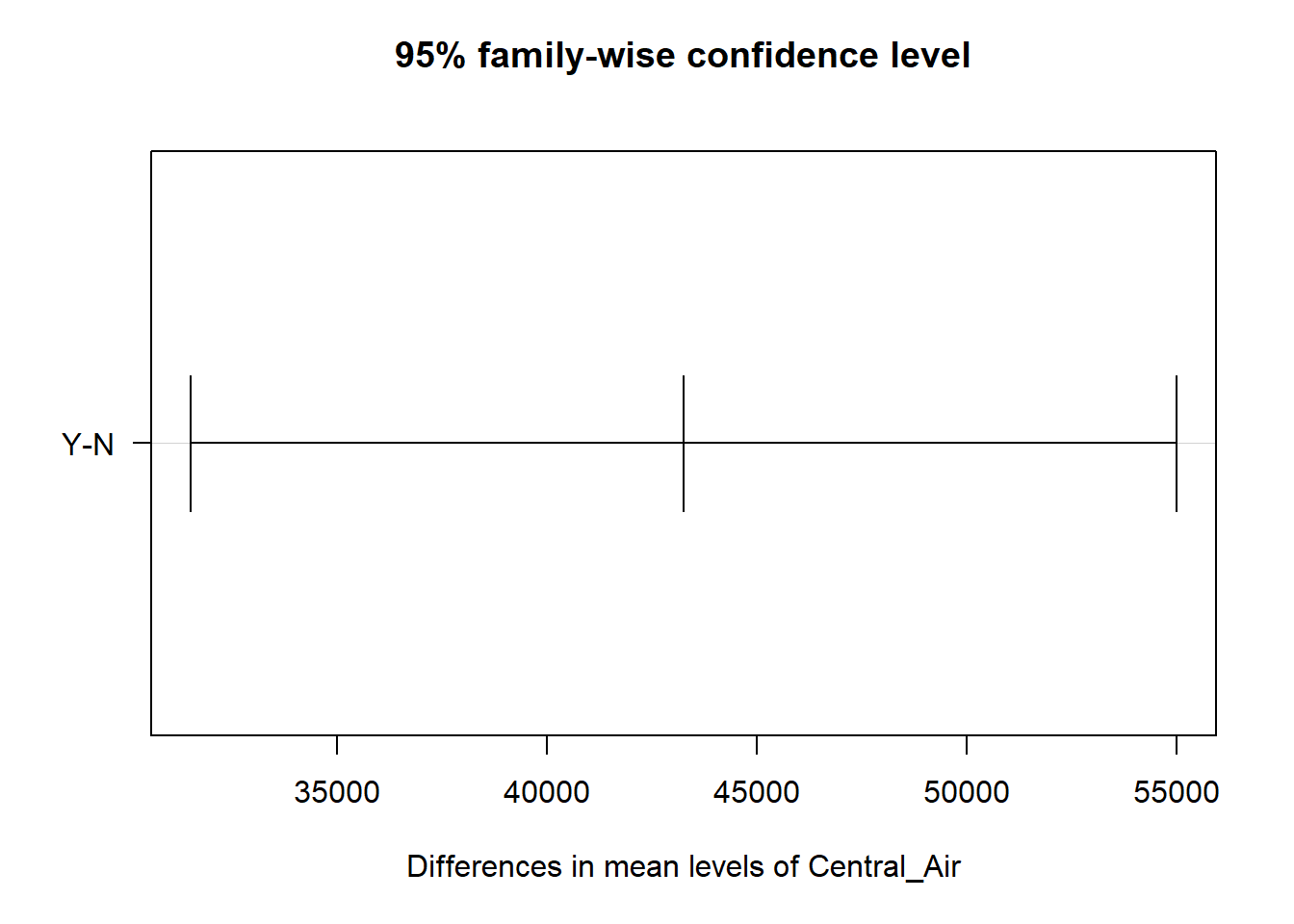
Starting with the variable for central air, we can see there is a statistical difference between the two categories. This is the exact same result as the overall F test for the variable since there are only two categories. For the heating quality variable, we can see some categories are different from each other, while others are not. Noticeably, the combination of poor with fair, good, and typical categories are not statistically different. Notice also the different widths of these confidence intervals do to the different combinations of sample sizes for the categories being tested.

3.1.4 Python Code

Two-way ANOVA model

import statsmodels.formula.api as smf
## C:\Users\sjsimmo2\AppData\Local\R\win-library\4.3\reticulate\python\rpytools\loader.py:117: UserWarning: Pandas requires version '2.8.4' or newer of 'numexpr' (version '2.8.3' currently installed).
##   return _find_and_load(name, import_)
## C:\Users\sjsimmo2\AppData\Local\R\win-library\4.3\reticulate\python\rpytools\loader.py:117: UserWarning: Pandas requires version '1.3.6' or newer of 'bottleneck' (version '1.3.5' currently installed).
##   return _find_and_load(name, import_)
import statsmodels.api as sm

train=r.train

model = smf.ols("Sale_Price ~ C(Heating_QC) + C(Central_Air)", data = train).fit()
model.summary()
OLS Regression Results
Dep. Variable: Sale_Price R-squared: 0.241
Model: OLS Adj. R-squared: 0.239
Method: Least Squares F-statistic: 129.9
Date: Tue, 18 Jun 2024 Prob (F-statistic): 9.06e-120
Time: 15:57:25 Log-Likelihood: -25788.
No. Observations: 2051 AIC: 5.159e+04
Df Residuals: 2045 BIC: 5.162e+04
Df Model: 5
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 5.264e+04 4.05e+04 1.301 0.193 -2.67e+04 1.32e+05
C(Heating_QC)[T.Fair] 3.833e+04 4.13e+04 0.927 0.354 -4.28e+04 1.19e+05
C(Heating_QC)[T.Typical] 4.161e+04 4.06e+04 1.024 0.306 -3.81e+04 1.21e+05
C(Heating_QC)[T.Good] 5.828e+04 4.08e+04 1.430 0.153 -2.17e+04 1.38e+05
C(Heating_QC)[T.Excellent] 1.14e+05 4.07e+04 2.803 0.005 3.42e+04 1.94e+05
C(Central_Air)[T.Y] 4.918e+04 6387.850 7.700 0.000 3.67e+04 6.17e+04
Omnibus: 806.993 Durbin-Watson: 1.995
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4426.691
Skew: 1.778 Prob(JB): 0.00
Kurtosis: 9.258 Cond. No. 88.5


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. 
sm.stats.anova_lm(model, typ=2)
##                       sum_sq      df           F        PR(>F)
## C(Heating_QC)   2.220229e+12     4.0  113.339043  2.254858e-87
## C(Central_Air)  2.903304e+11     1.0   59.283540  2.110570e-14
## Residual        1.001502e+13  2045.0         NaN           NaN

Post-hoc testing

from statsmodels.stats.multicomp import pairwise_tukeyhsd

train['anova_combo'] = train.Heating_QC.astype('string') + " / " + train.Central_Air

mcomp = pairwise_tukeyhsd(endog = train['Sale_Price'], groups = train['anova_combo'], alpha = 0.05)

mcomp.summary()
Multiple Comparison of Means - Tukey HSD, FWER=0.05
group1 group2 meandiff p-adj lower upper reject
Excellent / N Excellent / Y 101339.6201 0.0001 34220.4846 168458.7556 True
Excellent / N Fair / N -30313.4514 0.9685 -108720.0544 48093.1515 False
Excellent / N Fair / Y 30103.1061 0.9641 -46178.4107 106384.6228 False
Excellent / N Good / N -4250.8577 1.0 -85421.1634 76919.448 False
Excellent / N Good / Y 45050.8262 0.5268 -22854.8425 112956.4949 False
Excellent / N Poor / N -65011.7273 0.971 -235219.081 105195.6264 False
Excellent / N Poor / Y -8061.7273 1.0 -239327.9804 223204.5259 False
Excellent / N Typical / N -11592.5078 1.0 -82690.3122 59505.2966 False
Excellent / N Typical / Y 26941.045 0.9612 -40512.9182 94395.0082 False
Excellent / Y Fair / N -131653.0715 0.0 -173349.1196 -89957.0234 True
Excellent / Y Fair / Y -71236.514 0.0 -108784.2815 -33688.7466 True
Excellent / Y Good / N -105590.4778 0.0 -152276.4883 -58904.4673 True
Excellent / Y Good / Y -56288.7939 0.0 -70506.5603 -42071.0275 True
Excellent / Y Poor / N -166351.3474 0.0272 -323072.4637 -9630.2311 True
Excellent / Y Poor / Y -109401.3474 0.8653 -330930.2278 112127.5331 False
Excellent / Y Typical / N -112932.1278 0.0 -138345.9594 -87518.2963 True
Excellent / Y Typical / Y -74398.5751 0.0 -86273.0096 -62524.1405 True
Fair / N Fair / Y 60416.5575 0.0194 5167.5586 115665.5563 True
Fair / N Good / N 26062.5937 0.9455 -35761.3548 87886.5422 False
Fair / N Good / Y 75364.2776 0.0 32413.5859 118314.9693 True
Fair / N Poor / N -34698.2759 0.9996 -196575.1591 127178.6074 False
Fair / N Poor / Y 22251.7241 1.0 -202954.0971 247457.5454 False
Fair / N Typical / N 18720.9437 0.966 -29117.1151 66559.0024 False
Fair / N Typical / Y 57254.4964 0.0008 15021.58 99487.4129 True
Fair / Y Good / N -34353.9638 0.7089 -93459.5897 24751.6622 False
Fair / Y Good / Y 14947.7201 0.97 -23988.5911 53884.0313 False
Fair / Y Poor / N -95114.8333 0.6877 -255973.1553 65743.4886 False
Fair / Y Poor / Y -38164.8333 0.9999 -262639.6345 186309.9678 False
Fair / Y Typical / N -41695.6138 0.0849 -85964.7259 2573.4982 False
Fair / Y Typical / Y -3162.061 1.0 -41305.1291 34981.0071 False
Good / N Good / Y 49301.6839 0.0369 1491.7993 97111.5685 True
Good / N Poor / N -60760.8696 0.9755 -223994.2867 102472.5476 False
Good / N Poor / Y -3810.8696 1.0 -229993.7272 222371.988 False
Good / N Typical / N -7341.6501 1.0 -59586.2959 44902.9957 False
Good / N Typical / Y 31191.9027 0.5315 -15974.212 78358.0174 False
Good / Y Poor / N -110062.5535 0.4435 -267122.1275 46997.0205 False
Good / Y Poor / Y -53112.5535 0.9991 -274881.0056 168655.8987 False
Good / Y Typical / N -56643.3339 0.0 -84067.1251 -29219.5428 True
Good / Y Typical / Y -18109.7812 0.0101 -33832.4936 -2387.0688 True
Poor / N Poor / Y 56950.0 0.9997 -214233.7196 328133.7196 False
Poor / N Typical / N 53419.2195 0.9877 -105046.6372 211885.0762 False
Poor / N Typical / Y 91952.7723 0.6985 -64912.0329 248817.5775 False
Poor / Y Typical / N -3530.7805 1.0 -226297.3945 219235.8336 False
Poor / Y Typical / Y 35002.7723 1.0 -186627.7845 256633.3291 False
Typical / N Typical / Y 38533.5528 0.0002 12248.1645 64818.941 True 
mcomp.plot_simultaneous()

3.2 Two-Way ANOVA with Interactions

What if the relationship between a predictor and target variable changed depending on the value of another predictor variable? For our example, we would say that the average difference in sales price between having central air and not having central changed depending on what level of heating quality the home had. In the bar chart in Figure 3.1, a potential interaction effect is displayed when the differences between the two bars within each heating category is different across heating category. If the difference, was the same, then there is no interaction present. In other words, no matter the heating quality rating of the home, the average difference in sales price between having central air and not having central air is the same.

This interaction model is represented as follows:

\[ Y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha \beta)_{ij} + \varepsilon_{ijk} \]

with the interaction effect, \((\alpha \beta)_{ij}\), as the multiplication of the two variables involved in the interaction. Interactions can occur between more than two variables as well. Interactions are good to evaluate as they can mask the effects of individual variables. For example, imagine a hypothetical example as shown in Figure 3.2 where the impact of having central air is opposite depending on which category of heating quality you have.

fake_HQ <- c("Poor", "Poor", "Excellent", "Excellent")
fake_CA <- c("N", "Y", "N", "Y")
fake_mean <- c(100, 150, 150, 100)

fake_df <- as.data.frame(cbind(fake_HQ, fake_CA, fake_mean))
ggplot(data = fake_df, aes(x = fake_HQ, y = as.numeric(fake_mean), fill = fake_CA)) +
  geom_bar(stat = "identity", position = position_dodge()) +
  labs(y = "Fake Sales Price (Thousands $)", x = "Fake Heating Quality Category") +
  scale_fill_brewer(palette = "Paired") +
  theme_minimal()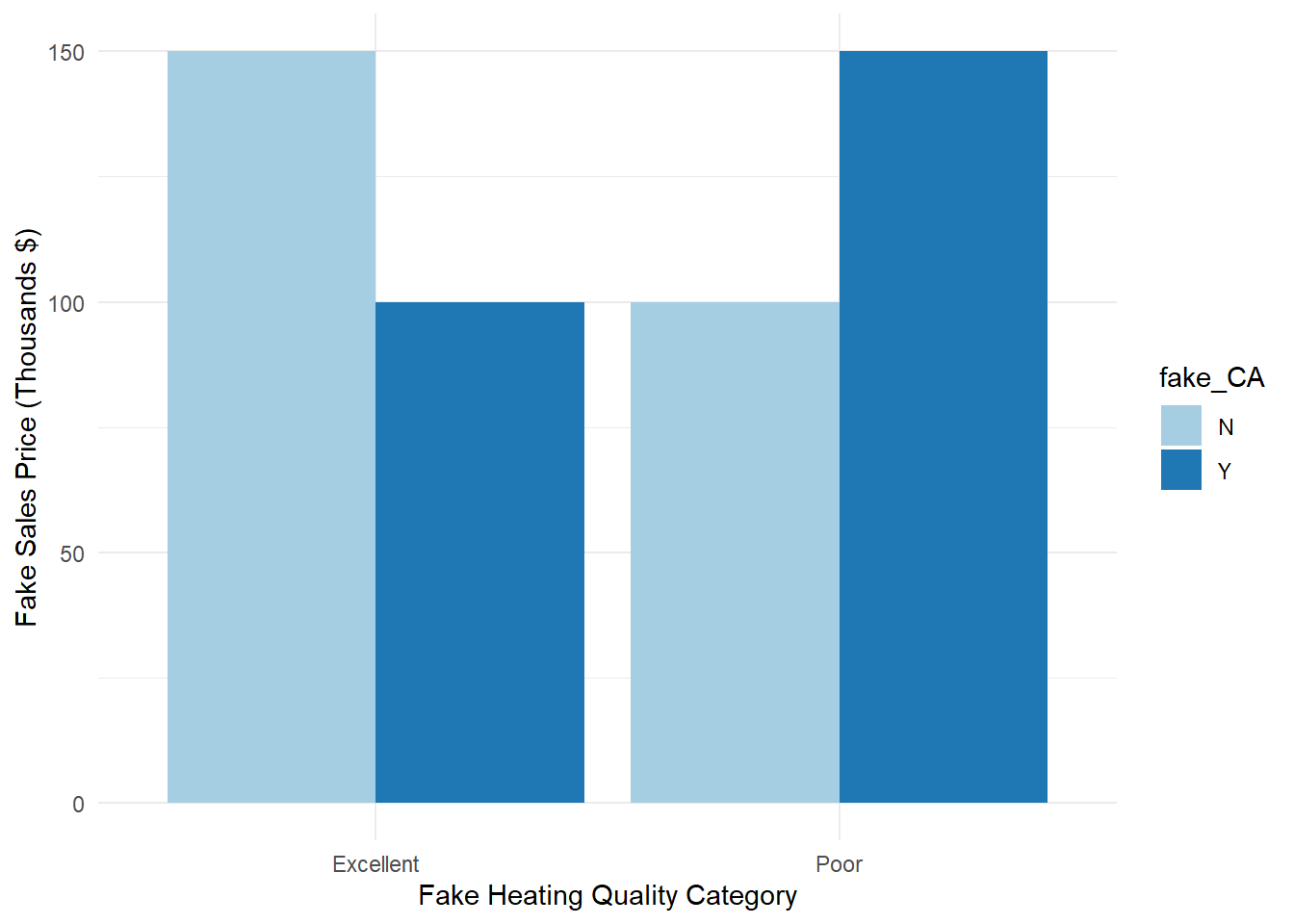
Distribution of Variables Heating_QC and Central_Air

Figure 3.2: Distribution of Variables Heating_QC and Central_Air

If you were to only look at the average sales price across heating quality, you would notice no difference between the two groups (average for both heating categories is 125). However, when the interaction is accounted for, you can clearly see in the bar heights that sales price is different depending on the value of central air.

Let’s evaluate the interaction term in our actual data. To do so, we just incorporate the multiplication of the two variables in the model statement by using the formula Sale_Price ~ Heating_QC + Central_Air + Heating_QC:Central_Air. You could also use the shorthand version of this by using the formula Sale_Price ~ Heating_QC*Central_Air. The * will include both main effects (the individual variables) and the interaction between them.

ames_aov_int <- aov(Sale_Price ~ Heating_QC*Central_Air, data = train)

summary(ames_aov_int)
##                          Df    Sum Sq   Mean Sq F value   Pr(>F)    
## Heating_QC                4 2.891e+12 7.228e+11 147.897  < 2e-16 ***
## Central_Air               1 2.903e+11 2.903e+11  59.403 1.99e-14 ***
## Heating_QC:Central_Air    4 3.972e+10 9.930e+09   2.032   0.0875 .  
## Residuals              2041 9.975e+12 4.887e+09                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

As seen by the output above, the interaction effect between heating quality and central air is not significant at the 0.05 level. Again, this implies that the average difference in sale price of the home between having central air and not does not differ depending on which category of heating quality the home belongs to. If our interaction was significant (say a 0.02 p-value instead) then we would keep it in our model, but here we would remove the interaction term from our model and rerun the analysis.

3.2.1 Post-Hoc Testing

Post-hoc tests are also available for interaction models as well to determine where the statistical differences exist in all the combinations of possible categories. We evaluate these post-hoc tests using the same TukeyHSD function and its corresponding plot element.

tukey.ames_int <- TukeyHSD(ames_aov_int)
print(tukey.ames_int)
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = Sale_Price ~ Heating_QC * Central_Air, data = train)
## 
## $Heating_QC
##                        diff        lwr       upr     p adj
## Fair-Poor          49176.42 -63536.973 161889.81 0.7565086
## Typical-Poor       67781.01 -42689.104 178251.13 0.4496163
## Good-Poor          87753.89 -22928.822 198436.60 0.1936558
## Excellent-Poor    146288.89  35929.963 256647.82 0.0027979
## Typical-Fair       18604.59  -6301.351  43510.54 0.2474998
## Good-Fair          38577.47  12744.901  64410.03 0.0004543
## Excellent-Fair     97112.47  72704.440 121520.50 0.0000000
## Good-Typical       19972.87   7063.227  32882.52 0.0002425
## Excellent-Typical  78507.88  68756.495  88259.26 0.0000000
## Excellent-Good     58535.00  46614.230  70455.77 0.0000000
## 
## $Central_Air
##         diff      lwr      upr p adj
## Y-N 43256.57 31520.09 54993.05     0
## 
## $`Heating_QC:Central_Air`
##                               diff         lwr       upr     p adj
## Fair:N-Poor:N            34698.276 -127178.615 196575.17 0.9996249
## Typical:N-Poor:N         53419.220 -105046.645 211885.08 0.9876643
## Good:N-Poor:N            60760.870 -102472.555 223994.29 0.9755371
## Excellent:N-Poor:N       65011.727 -105195.635 235219.09 0.9709555
## Poor:Y-Poor:N            56950.000 -214233.733 328133.73 0.9996829
## Fair:Y-Poor:N            95114.833  -65743.496 255973.16 0.6876708
## Typical:Y-Poor:N         91952.772  -64912.040 248817.58 0.6985070
## Good:Y-Poor:N           110062.553  -46997.028 267122.13 0.4435353
## Excellent:Y-Poor:N      166351.347    9630.224 323072.47 0.0271785
## Typical:N-Fair:N         18720.944  -29117.117  66559.00 0.9659507
## Good:N-Fair:N            26062.594  -35761.358  87886.55 0.9454988
## Excellent:N-Fair:N       30313.451  -48093.155 108720.06 0.9685428
## Poor:Y-Fair:N            22251.724 -202954.108 247457.56 0.9999995
## Fair:Y-Fair:N            60416.557    5167.556 115665.56 0.0193847
## Typical:Y-Fair:N         57254.496   15021.578  99487.41 0.0007697
## Good:Y-Fair:N            75364.278   32413.584 118314.97 0.0000014
## Excellent:Y-Fair:N      131653.071   89957.021 173349.12 0.0000000
## Good:N-Typical:N          7341.650  -44902.998  59586.30 0.9999894
## Excellent:N-Typical:N    11592.508  -59505.300  82690.32 0.9999620
## Poor:Y-Typical:N          3530.780 -219235.844 226297.41 1.0000000
## Fair:Y-Typical:N         41695.614   -2573.500  85964.73 0.0848888
## Typical:Y-Typical:N      38533.553   12248.163  64818.94 0.0001576
## Good:Y-Typical:N         56643.334   29219.541  84067.13 0.0000000
## Excellent:Y-Typical:N   112932.128   87518.295 138345.96 0.0000000
## Excellent:N-Good:N        4250.858  -76919.452  85421.17 1.0000000
## Poor:Y-Good:N            -3810.870 -229993.738 222372.00 1.0000000
## Fair:Y-Good:N            34353.964  -24751.665  93459.59 0.7089196
## Typical:Y-Good:N         31191.903  -15974.214  78358.02 0.5315494
## Good:Y-Good:N            49301.684    1491.797  97111.57 0.0369201
## Excellent:Y-Good:N      105590.478   58904.465 152276.49 0.0000000
## Poor:Y-Excellent:N       -8061.727 -239327.991 223204.54 1.0000000
## Fair:Y-Excellent:N       30103.106  -46178.414 106384.63 0.9640522
## Typical:Y-Excellent:N    26941.045  -40512.921  94395.01 0.9611660
## Good:Y-Excellent:N       45050.826  -22854.846 112956.50 0.5267698
## Excellent:Y-Excellent:N 101339.620   34220.481 168458.76 0.0000809
## Fair:Y-Poor:Y            38164.833 -186309.978 262639.65 0.9999458
## Typical:Y-Poor:Y         35002.772 -186627.795 256633.34 0.9999711
## Good:Y-Poor:Y            53112.553 -168655.909 274881.02 0.9990789
## Excellent:Y-Poor:Y      109401.347 -112127.544 330930.24 0.8652766
## Typical:Y-Fair:Y         -3162.061  -41305.131  34981.01 0.9999999
## Good:Y-Fair:Y            14947.720  -23988.593  53884.03 0.9699661
## Excellent:Y-Fair:Y       71236.514   33688.745 108784.28 0.0000001
## Good:Y-Typical:Y         18109.781    2387.068  33832.49 0.0101482
## Excellent:Y-Typical:Y    74398.575   62524.140  86273.01 0.0000000
## Excellent:Y-Good:Y       56288.794   42071.027  70506.56 0.0000000
plot(tukey.ames_int, las = 1)

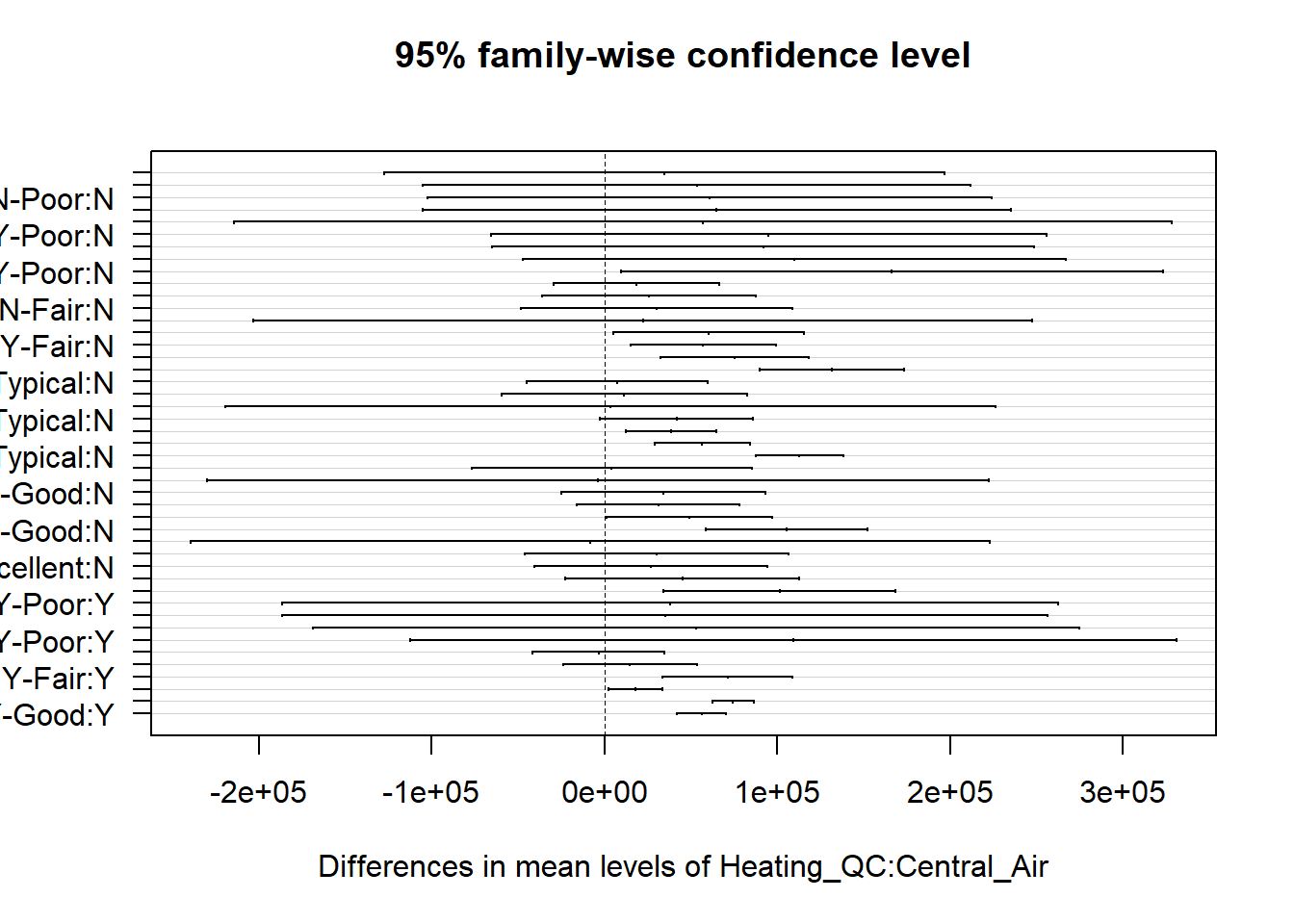
In the giant table above as well as the confidence interval plots, you are able to inspect which combination of categories are statistically different.

With interactions present in ANOVA models, post-hoc tests might get overwhelming in trying to find where differences exist. To help guide the exploration of post-hoc tests with interactions, we can do slicing. Slicing is when you perform One-Way ANOVA on subsets of data within categories of other variables. Even though the interaction in our model was not significant, let’s imagine that it was for the sake of example. For example, to help discover differences in the interaction between central air and heating quality, we could subset the data into two groups - homes with central air and homes without. Within these two groups we perform One-Way ANOVA across heating quality to find where differences might exist within subgroups.

This can easily be done with the group_by function to subset the data. The nest and mutate functions are also used to applied the aov function to each subgroup. Here we run a One-Way ANOVA for heating quality within each subset of central air being present or not.

CA_aov <- train %>% 
  group_by(Central_Air) %>%
  nest() %>%
  mutate(aov = map(data, ~summary(aov(Sale_Price ~ Heating_QC, data = .x))))

CA_aov
## # A tibble: 2 × 3
## # Groups:   Central_Air [2]
##   Central_Air data                  aov       
##   <fct>       <list>                <list>    
## 1 Y           <tibble [1,904 × 81]> <summry.v>
## 2 N           <tibble [147 × 81]>   <summry.v>
print(CA_aov$aov)
## [[1]]
##               Df    Sum Sq   Mean Sq F value Pr(>F)    
## Heating_QC     4 2.242e+12 5.606e+11   108.5 <2e-16 ***
## Residuals   1899 9.809e+12 5.165e+09                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## [[2]]
##              Df    Sum Sq   Mean Sq F value  Pr(>F)   
## Heating_QC    4 1.774e+10 4.435e+09   3.793 0.00582 **
## Residuals   142 1.660e+11 1.169e+09                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

We can see that both of these results are significant at the 0.05 level. This implies that there are statistical differences in average sale price across heating quality within homes that have central air as well as those that don’t have central air.

3.2.2 Assumptions

The assumptions for the \(n\)-Way ANOVA are the same as with the One-Way ANOVA - independence of observations, normality for each category of variable, and equal variances. With the inclusion of two or more variables (\(n\)-Way ANOVA with \(n > 1\)), these assumptions can be harder to evaluate and test. These assumptions are then applied to the residuals of the model.

For equal variances, we can still apply the Levene Test for equal variances using the same leveneTest function as in Chapter 2.

leveneTest(Sale_Price ~ Heating_QC*Central_Air, data = train)
## Levene's Test for Homogeneity of Variance (center = median)
##         Df F value    Pr(>F)    
## group    9   24.17 < 2.2e-16 ***
##       2041                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

From this test, we can see that we do not meet our assumption of equal variance.

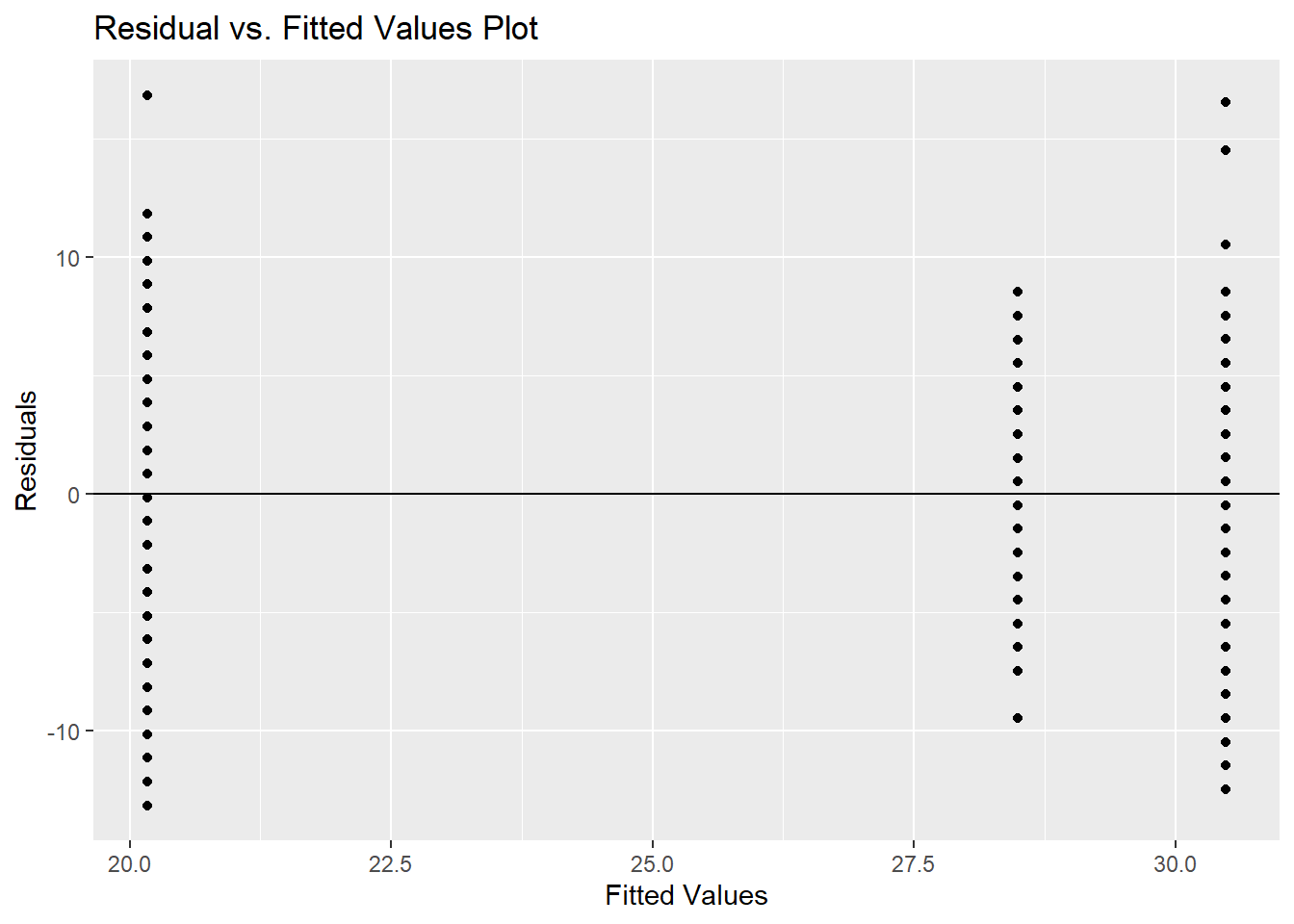
Let’s explore the normality assumption. Again, we will assume this normality on the random error component, \(\varepsilon_{ijk}\), of the ANOVA model. More details are found for diagnostic testing using the error component in Diagnostic chapter. We can check normality using the same approaches of the QQ-plot or statistical testing as in the section on EDA. Here we will use the plot function on the aov object. Specifically, we want the second plot which is why we have a 2 in the plot function option. We then use the shapiro.test function on the error component. The estimate of the error component is calculated using the residuals function.

plot(ames_aov_int, 2)

ames_res <- residuals(ames_aov_int)

shapiro.test(x = ames_res)
## 
##  Shapiro-Wilk normality test
## 
## data:  ames_res
## W = 0.8838, p-value < 2.2e-16

Neither of the normality or equal variance assumptions appear to be met here. This would be a good scenario to have a non-parametric approach. Unfortunately, the Kruskal-Wallis approach is not applicable to \(n\)-Way ANOVA where \(n > 1\). These approaches would need more non-parametric versions of multiple regression models to account for them.

3.2.3 Python Code

Two-way ANOVA with interactions

train=r.train
import matplotlib.pyplot as plt
import scipy as sp
import pandas as pd
import numpy as np


model = smf.ols("Sale_Price ~ C(Heating_QC)*C(Central_Air)", data = train).fit()
model.summary()
OLS Regression Results
Dep. Variable: Sale_Price R-squared: 0.244
Model: OLS Adj. R-squared: 0.241
Method: Least Squares F-statistic: 73.24
Date: Tue, 18 Jun 2024 Prob (F-statistic): 1.99e-117
Time: 15:57:28 Log-Likelihood: -25784.
No. Observations: 2051 AIC: 5.159e+04
Df Residuals: 2041 BIC: 5.164e+04
Df Model: 9
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 5.005e+04 4.94e+04 1.012 0.311 -4.69e+04 1.47e+05
C(Heating_QC)[T.Fair] 3.47e+04 5.11e+04 0.679 0.497 -6.55e+04 1.35e+05
C(Heating_QC)[T.Typical] 5.342e+04 5e+04 1.068 0.286 -4.47e+04 1.52e+05
C(Heating_QC)[T.Good] 6.076e+04 5.15e+04 1.179 0.239 -4.03e+04 1.62e+05
C(Heating_QC)[T.Excellent] 6.501e+04 5.37e+04 1.210 0.227 -4.04e+04 1.7e+05
C(Central_Air)[T.Y] 5.695e+04 8.56e+04 0.665 0.506 -1.11e+05 2.25e+05
C(Heating_QC)[T.Fair]:C(Central_Air)[T.Y] 3466.5575 8.74e+04 0.040 0.968 -1.68e+05 1.75e+05
C(Heating_QC)[T.Typical]:C(Central_Air)[T.Y] -1.842e+04 8.6e+04 -0.214 0.831 -1.87e+05 1.5e+05
C(Heating_QC)[T.Good]:C(Central_Air)[T.Y] -7648.3161 8.69e+04 -0.088 0.930 -1.78e+05 1.63e+05
C(Heating_QC)[T.Excellent]:C(Central_Air)[T.Y] 4.439e+04 8.82e+04 0.503 0.615 -1.29e+05 2.17e+05
Omnibus: 806.508 Durbin-Watson: 1.995
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4446.618
Skew: 1.774 Prob(JB): 0.00
Kurtosis: 9.280 Cond. No. 217.


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. 
sm.stats.anova_lm(model, typ=2)
##                                     sum_sq      df           F        PR(>F)
## C(Heating_QC)                 2.220229e+12     4.0  113.567764  1.612447e-87
## C(Central_Air)                2.903304e+11     1.0   59.403176  1.991166e-14
## C(Heating_QC):C(Central_Air)  3.971968e+10     4.0    2.031716  8.746590e-02
## Residual                      9.975296e+12  2041.0         NaN           NaN
train['resid_anova_2way'] = model.resid

Post-hoc testing

model_slice1 = smf.ols("Sale_Price ~ C(Heating_QC)", data = train[train["Central_Air"] == 'Y']).fit()
model_slice1.summary()
OLS Regression Results
Dep. Variable: Sale_Price R-squared: 0.186
Model: OLS Adj. R-squared: 0.184
Method: Least Squares F-statistic: 108.5
Date: Tue, 18 Jun 2024 Prob (F-statistic): 2.29e-83
Time: 15:57:28 Log-Likelihood: -23991.
No. Observations: 1904 AIC: 4.799e+04
Df Residuals: 1899 BIC: 4.802e+04
Df Model: 4
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 1.07e+05 7.19e+04 1.489 0.137 -3.4e+04 2.48e+05
C(Heating_QC)[T.Fair] 3.816e+04 7.29e+04 0.524 0.600 -1.05e+05 1.81e+05
C(Heating_QC)[T.Typical] 3.5e+04 7.19e+04 0.487 0.627 -1.06e+05 1.76e+05
C(Heating_QC)[T.Good] 5.311e+04 7.2e+04 0.738 0.461 -8.81e+04 1.94e+05
C(Heating_QC)[T.Excellent] 1.094e+05 7.19e+04 1.521 0.128 -3.16e+04 2.5e+05
Omnibus: 730.142 Durbin-Watson: 2.004
Prob(Omnibus): 0.000 Jarque-Bera (JB): 3727.430
Skew: 1.749 Prob(JB): 0.00
Kurtosis: 8.895 Cond. No. 116.


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. 
sm.stats.anova_lm(model_slice1, typ=2)
##                      sum_sq      df           F        PR(>F)
## C(Heating_QC)  2.242210e+12     4.0  108.518706  2.294916e-83
## Residual       9.809268e+12  1899.0         NaN           NaN
model_slice2 = smf.ols("Sale_Price ~ C(Heating_QC)", data = train[train["Central_Air"] == 'N']).fit()
model_slice2.summary()
OLS Regression Results
Dep. Variable: Sale_Price R-squared: 0.097
Model: OLS Adj. R-squared: 0.071
Method: Least Squares F-statistic: 3.793
Date: Tue, 18 Jun 2024 Prob (F-statistic): 0.00582
Time: 15:57:28 Log-Likelihood: -1740.7
No. Observations: 147 AIC: 3491.
Df Residuals: 142 BIC: 3506.
Df Model: 4
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 5.005e+04 2.42e+04 2.070 0.040 2253.387 9.78e+04
C(Heating_QC)[T.Fair] 3.47e+04 2.5e+04 1.388 0.167 -1.47e+04 8.41e+04
C(Heating_QC)[T.Typical] 5.342e+04 2.45e+04 2.183 0.031 5043.233 1.02e+05
C(Heating_QC)[T.Good] 6.076e+04 2.52e+04 2.410 0.017 1.09e+04 1.11e+05
C(Heating_QC)[T.Excellent] 6.501e+04 2.63e+04 2.473 0.015 1.31e+04 1.17e+05
Omnibus: 10.251 Durbin-Watson: 1.957
Prob(Omnibus): 0.006 Jarque-Bera (JB): 11.172
Skew: 0.516 Prob(JB): 0.00375
Kurtosis: 3.871 Cond. No. 23.0


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. 
sm.stats.anova_lm(model_slice2, typ=2)
##                      sum_sq     df         F   PR(>F)
## C(Heating_QC)  1.773945e+10    4.0  3.793029  0.00582
## Residual       1.660284e+11  142.0       NaN      NaN

Assumptions

sm.qqplot(train['resid_anova_2way'])
plt.show()

sp.stats.shapiro(model.resid)
## ShapiroResult(statistic=0.8838016140166404, pvalue=1.0540317548240295e-36)

3.3 Randomized Block Design

There are two typical groups of data analysis studies that are conducted. The first are observational/retrospective studies which are the typical data problems people try to solve. The primary characteristic of these analysis are looking at what already happened (retrospective) and potentially inferring those results to further data. These studies have little control over other factors contributing to the target of interest because data is collected after the fact.

The other type of data analysis study are controlled experiments. In these situations, you often want to look at the outcome measure prospectively. The focus of the controlled experiment is to control for other factors that might contribute to the target variable. By manipulating these factors of interest, one can more reasonably claim causation. We can more reasonably claim causation when random assignment is used to eliminate potential nuisance factors. Nuisance factors are variables that can potentially impact the target variable, but are not of interest in the analysis directly.

3.3.1 Garlic Bulb Weight Example

For this analysis we will use a new dataset. This dataset contains the average garlic bulb weight from different plots of land. We want to compare the effects of fertilizer on average bulb weight. However, different plots of land could have different levels of sun exposure, pH for the soil, and rain amounts. Since we cannot alter the pH of the soil easily, or control the sun and rain, we can use blocking to account for these nuisance factors. Each fertilizer was randomly applied in quadrants of 8 plots of land. These 8 plots have different values for sun exposure, pH, and rain amount. Therefore, if we only put one fertilizer on each plot, we would not know if the fertilizer was the reason the garlic crop grew or if it was one of the nuisance factors. Since we blocked these 8 plots and applied all four fertilizers in each we have essentially accounted for (or removed the effect of) the nuisance factors.

Let’s briefly explore this new dataset by looking at all 32 values using the print function.

block <- read_csv(file = "garlic_block.csv")
## Rows: 32 Columns: 6
## ── Column specification ────────────────────────────────────────────────────────
## Delimiter: ","
## dbl (6): Sector, Position, Fertilizer, BulbWt, Cloves, BedId
## 
## ℹ Use `spec()` to retrieve the full column specification for this data.
## ℹ Specify the column types or set `show_col_types = FALSE` to quiet this message.
head(block, n = 32)
## # A tibble: 32 × 6
##    Sector Position Fertilizer BulbWt Cloves BedId
##     <dbl>    <dbl>      <dbl>  <dbl>  <dbl> <dbl>
##  1      1        1          3  0.259   11.6 22961
##  2      1        2          4  0.207   12.6 23884
##  3      1        3          1  0.275   12.1 19642
##  4      1        4          2  0.245   12.1 20384
##  5      2        1          3  0.215   11.6 20303
##  6      2        2          4  0.170   12.7 21004
##  7      2        3          1  0.225   12.0 16117
##  8      2        4          2  0.168   11.9 19686
##  9      3        1          4  0.217   12.4 26527
## 10      3        2          3  0.226   11.7 23574
## # ℹ 22 more rows

How do we account for this blocking in an ANOVA model context? This blocking ANOVA model is the exact same as the Two-Way ANOVA model. The variable that identifies which sector (block) an observation is in serves as another variable in the model. Think about this variable as the variable that accounts for all the nuisance factors in your ANOVA. That means we have two variables in this ANOVA model - fertilizer and sector (the block that accounts for sun exposure, pH level of soil, rain amount, etc.).

For this we can use the same aov function we described above.

block_aov <- aov(BulbWt ~ factor(Fertilizer) + factor(Sector), data = block)

summary(block_aov)
##                    Df   Sum Sq   Mean Sq F value   Pr(>F)    
## factor(Fertilizer)  3 0.005086 0.0016954   4.307 0.016222 *  
## factor(Sector)      7 0.017986 0.0025695   6.527 0.000364 ***
## Residuals          21 0.008267 0.0003937                     
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Using the summary function we can see that both the sector (block) and fertilizer variables are significant in the model at the 0.05 level. What are the interpretations of this? First, let’s address the blocking variable. Whether it is significant or not, it should always be included in the model. This is due to the fact that the data is structured in that way. It is a construct of the data that should be accounted for regardless of the significance. However, since the blocking variable (sector) was significant, that implies that different plots of land have different impacts of the average bulb weight of garlic. Again, this is most likely due to the differences between the plots of land - namely sun exposure, pH of soil, rain fall, etc.

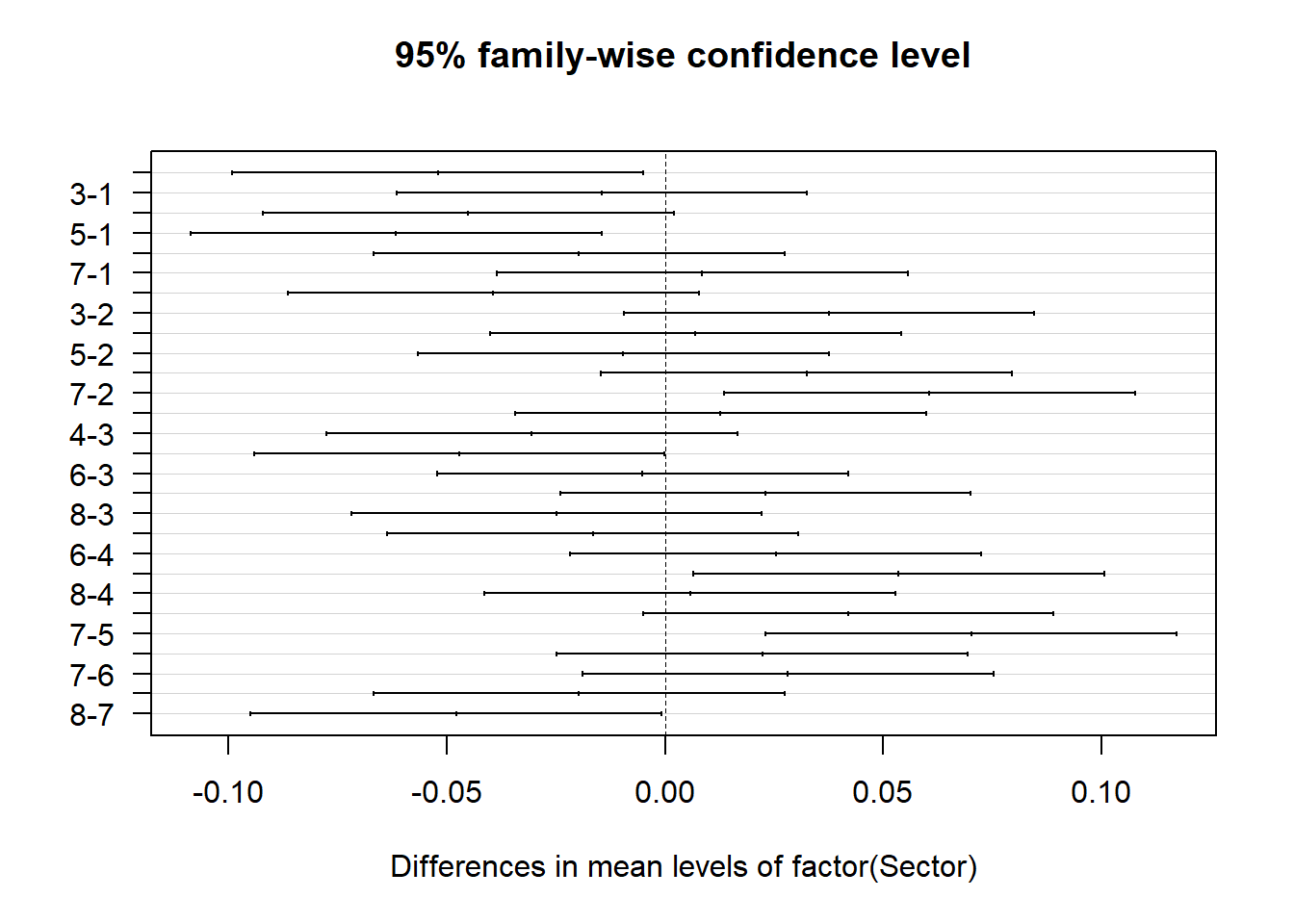
Second, the variable of interest is the fertilizer variable. It is significant, implying that there is a difference in the average bulb weight of garlic for different fertilizers. To examine which fertilizer pairs are statistically difference we can use post-hos testing as described in the previous parts of this chapter using the TukeyHSD function.

tukey.block <- TukeyHSD(block_aov)
print(tukey.block)
##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = BulbWt ~ factor(Fertilizer) + factor(Sector), data = block)
## 
## $`factor(Fertilizer)`
##            diff         lwr          upr     p adj
## 2-1 -0.02509875 -0.05275125  0.002553751 0.0840024
## 3-1 -0.01294875 -0.04060125  0.014703751 0.5698678
## 4-1 -0.03336125 -0.06101375 -0.005708749 0.0144260
## 3-2  0.01215000 -0.01550250  0.039802501 0.6186232
## 4-2 -0.00826250 -0.03591500  0.019390001 0.8382800
## 4-3 -0.02041250 -0.04806500  0.007240001 0.1995492
## 
## $`factor(Sector)`
##           diff          lwr           upr     p adj
## 2-1 -0.0520675 -0.099126544 -5.008456e-03 0.0234315
## 3-1 -0.0145075 -0.061566544  3.255154e-02 0.9634255
## 4-1 -0.0450550 -0.092114044  2.004044e-03 0.0669646
## 5-1 -0.0616250 -0.108684044 -1.456596e-02 0.0051483
## 6-1 -0.0196650 -0.066724044  2.739404e-02 0.8466335
## 7-1  0.0084950 -0.038564044  5.555404e-02 0.9984089
## 8-1 -0.0393325 -0.086391544  7.726544e-03 0.1469768
## 3-2  0.0375600 -0.009499044  8.461904e-02 0.1841786
## 4-2  0.0070125 -0.040046544  5.407154e-02 0.9995370
## 5-2 -0.0095575 -0.056616544  3.750154e-02 0.9966777
## 6-2  0.0324025 -0.014656544  7.946154e-02 0.3337758
## 7-2  0.0605625  0.013503456  1.076215e-01 0.0061094
## 8-2  0.0127350 -0.034324044  5.979404e-02 0.9819446
## 4-3 -0.0305475 -0.077606544  1.651154e-02 0.4025951
## 5-3 -0.0471175 -0.094176544 -5.845586e-05 0.0495704
## 6-3 -0.0051575 -0.052216544  4.190154e-02 0.9999400
## 7-3  0.0230025 -0.024056544  7.006154e-02 0.7227812
## 8-3 -0.0248250 -0.071884044  2.223404e-02 0.6454690
## 5-4 -0.0165700 -0.063629044  3.048904e-02 0.9286987
## 6-4  0.0253900 -0.021669044  7.244904e-02 0.6208608
## 7-4  0.0535500  0.006490956  1.006090e-01 0.0186102
## 8-4  0.0057225 -0.041336544  5.278154e-02 0.9998793
## 6-5  0.0419600 -0.005099044  8.901904e-02 0.1034664
## 7-5  0.0701200  0.023060956  1.171790e-01 0.0012997
## 8-5  0.0222925 -0.024766544  6.935154e-02 0.7514897
## 7-6  0.0281600 -0.018899044  7.521904e-02 0.5004099
## 8-6 -0.0196675 -0.066726544  2.739154e-02 0.8465530
## 8-7 -0.0478275 -0.094886544 -7.684559e-04 0.0446174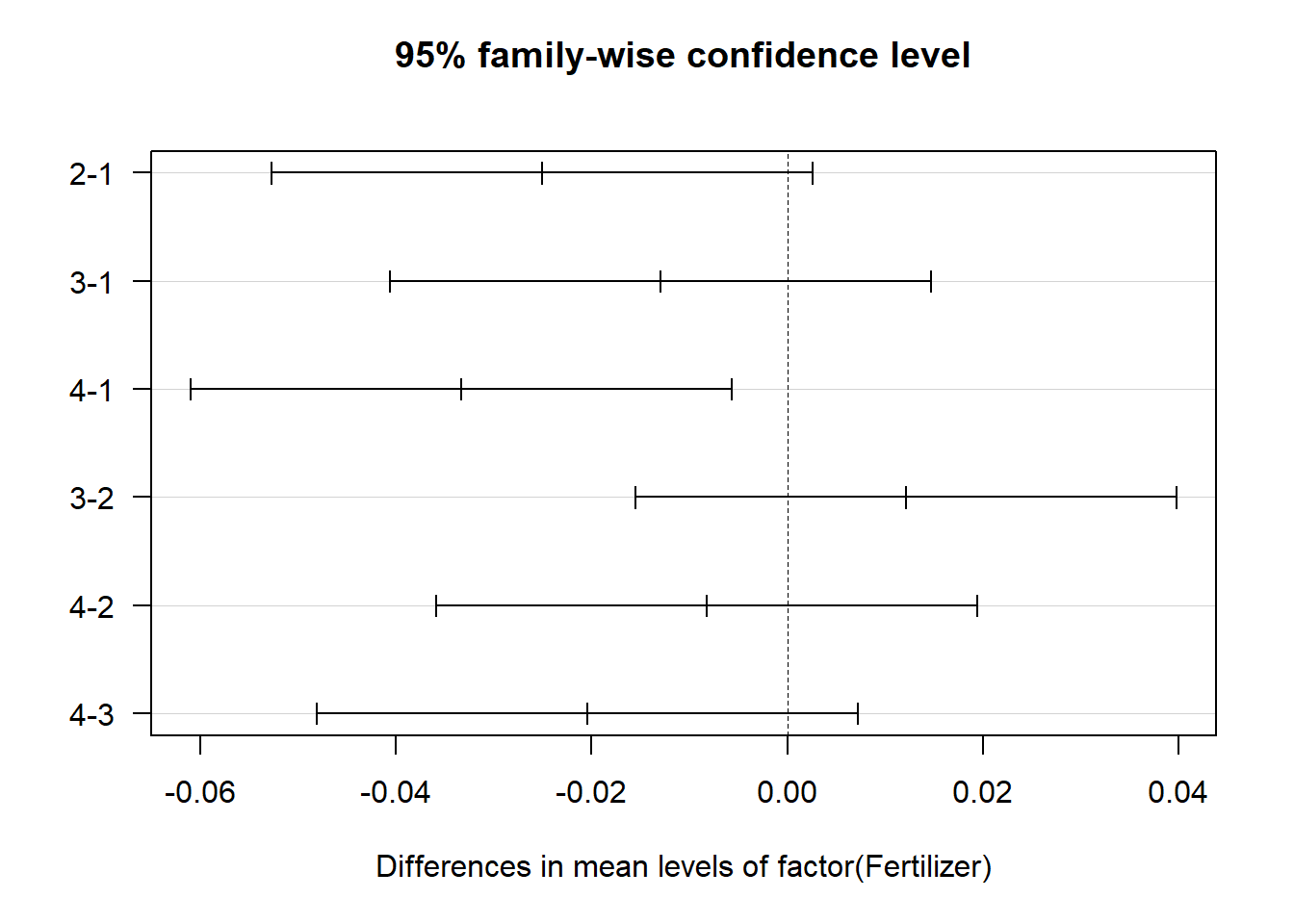
plot(tukey.block, las = 1)

3.3.2 Assumptions

Outside of the typical assumptions for ANOVA that still hold here, there are two additional assumptions to be met:

  • Treatments are randomly assigned within each block
  • The effects of the treatment variable are constant across the levels of the blocking variable

The first, new assumption of randomness deals with the reliability of the analysis. Randomness is key to removing the impact of the nuisance factors. The second, new assumption implies there is no interaction between the treatment variable and the blocking variable. For example, we are implying that the fertilizers’ impacts ob garlic bulb weight are not changed depending on what block you are on. In other words, fertilizers have the same impact regardless of sun exposure, pH levels, rain fall, etc. We are not saying these nuisance factors do not impact the target variable or bulb weight of garlic, just that they do not change the effect of the fertilizer on bulb weight.

3.3.3 Python Code

block=pd.read_csv('https://raw.githubusercontent.com/IAA-Faculty/statistical_foundations/master/garlic_block.csv')
block.head(n = 32)
##     Sector  Position  Fertilizer   BulbWt   Cloves  BedId
## 0        1         1           3  0.25881  11.6322  22961
## 1        1         2           4  0.20746  12.5837  23884
## 2        1         3           1  0.27453  12.0597  19642
## 3        1         4           2  0.24467  12.1001  20384
## 4        2         1           3  0.21454  11.5863  20303
## 5        2         2           4  0.16953  12.7132  21004
## 6        2         3           1  0.22504  12.0470  16117
## 7        2         4           2  0.16809  11.9071  19686
## 8        3         1           4  0.21720  12.3655  26527
## 9        3         2           3  0.22551  11.6864  23574
## 10       3         3           2  0.23536  12.0258  17499
## 11       3         4           1  0.24937  11.6668  16636
## 12       4         1           4  0.20811  12.5996  24834
## 13       4         2           1  0.21138  12.1393  19946
## 14       4         3           2  0.19320  12.0792  21504
## 15       4         4           3  0.19256  11.6464  23181
## 16       5         1           4  0.19851  12.5355  24533
## 17       5         2           1  0.18603  12.3307  15009
## 18       5         3           3  0.19698  11.5608  23845
## 19       5         4           2  0.15745  11.8735  18948
## 20       6         1           2  0.20058  11.9077  20019
## 21       6         2           3  0.25346  11.7294  22228
## 22       6         3           4  0.19838  12.7670  24424
## 23       6         4           1  0.25439  12.0139  13755
## 24       7         1           3  0.26578  11.7448  21087
## 25       7         2           4  0.21678  12.8531  25751
## 26       7         3           2  0.26183  12.3990  20296
## 27       7         4           1  0.27506  11.9383  20038
## 28       8         1           1  0.21420  12.1034  17843
## 29       8         2           3  0.17877  11.5682  21394
## 30       8         3           4  0.20714  12.5213  27191
## 31       8         4           2  0.22803  12.2317  20202
import statsmodels.formula.api as smf

model_b = smf.ols("BulbWt ~ C(Fertilizer) + C(Sector)", data = block).fit()
model_b.summary()
OLS Regression Results
Dep. Variable: BulbWt R-squared: 0.736
Model: OLS Adj. R-squared: 0.611
Method: Least Squares F-statistic: 5.861
Date: Tue, 18 Jun 2024 Prob (F-statistic): 0.000328
Time: 15:57:30 Log-Likelihood: 86.773
No. Observations: 32 AIC: -151.5
Df Residuals: 21 BIC: -135.4
Df Model: 10
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 0.2642 0.012 22.713 0.000 0.240 0.288
C(Fertilizer)[T.2] -0.0251 0.010 -2.530 0.019 -0.046 -0.004
C(Fertilizer)[T.3] -0.0129 0.010 -1.305 0.206 -0.034 0.008
C(Fertilizer)[T.4] -0.0334 0.010 -3.363 0.003 -0.054 -0.013
C(Sector)[T.2] -0.0521 0.014 -3.711 0.001 -0.081 -0.023
C(Sector)[T.3] -0.0145 0.014 -1.034 0.313 -0.044 0.015
C(Sector)[T.4] -0.0451 0.014 -3.211 0.004 -0.074 -0.016
C(Sector)[T.5] -0.0616 0.014 -4.392 0.000 -0.091 -0.032
C(Sector)[T.6] -0.0197 0.014 -1.402 0.176 -0.049 0.010
C(Sector)[T.7] 0.0085 0.014 0.605 0.551 -0.021 0.038
C(Sector)[T.8] -0.0393 0.014 -2.803 0.011 -0.069 -0.010
Omnibus: 1.984 Durbin-Watson: 2.574
Prob(Omnibus): 0.371 Jarque-Bera (JB): 1.162
Skew: -0.071 Prob(JB): 0.559
Kurtosis: 2.077 Cond. No. 9.67


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified. 
sm.stats.anova_lm(model_b, typ=2)
##                  sum_sq    df         F    PR(>F)
## C(Fertilizer)  0.005086   3.0  4.306540  0.016222
## C(Sector)      0.017986   7.0  6.526673  0.000364
## Residual       0.008267  21.0       NaN       NaN

3.4 Multiple Linear Regression

Most practical applications of of regression modeling involve using more complicated models than a simple linear regression with only one predictor variable to predict your target. Additional variables in a model can lead to better explanations and predictions of the target. These linear regressions with more than one variable are called multiple linear regression models. However, as we will see in this section and the following chapters, with more variables comes much more complication.

3.4.1 Model Structure

Multiple linear regression models have the same structure as simple linear regression models, only with more variables. The multiple linear regression model with \(k\) variables is structured like the following:

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k + \varepsilon \]

This model has the predictor variables \(x_1, x_2, ..., x_k\) trying to either explain or predict the target variable \(y\). The intercept, \(\beta_0\), still gives the expected value of \(y\), when all of the predictor variables take a value of 0. With the addition of multiple predictors, the interpretation of the slope coefficients change slightly. The slopes, \(\beta_1, \beta_2, ..., \beta_k\), give the expected change in \(y\) for a one unit change in the respective predictor variable, holding all other predictor variables constant. The random error term, \(\varepsilon\), is the error between our predicted value, \(\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \cdots + \hat{\beta}_k x_k\), and our actual value of \(y\).

Unlike simple linear regression that can be visualized as a line through a 2-dimensional scatterplot of data, a multiple linear regression is better thought of as a multi-dimensional plane through a multi-dimensional scatterplot of data.

Let’s visual an example with two predictor variables - the square footage of greater living area and the total number of rooms. These will predict sale price of a home. When none of the variables have any relationship with the target variable, we get a horizontal plane like the one shown below. This is similar in concept to a horizontal line in simple linear regression having a slope of 0, implying that the target variable does not change as the predictor variable changes.

Much like if the slope of a simple linear regression line is not 0 (a relationship exists between the predictor and target variable), then a relationship between any of the predictor variables and the target variable shifts and rotates the plane around like the one shown below.

To the naive viewer, the shifted plane would still make sense because of the model naming convention of multiple linear regression. However, the linear in linear regression doesn’t have to deal with the visualization of the fitted plane (or line in two dimensions), but instead refers to the linear combination of variables. A linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results. For example, \(ax + by\) is a linear combination of \(x\) and \(y\). Therefore, the linear model

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \cdots + \beta_k x_k + \varepsilon \] is a linear combination of predictor variables in their relationship with the target variable \(y\). These predictor variables do not all have to contain linear effects though. For example, let’s look at a linear regression model with four predictor variables:

\[ y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \beta_3 x_3 + \beta_4 x_4 + \varepsilon \]

One would not be hard pressed to call this model a linear regression. However, what if we defined \(x_3 = x_1^2\) and \(x_4 = x_2^2\)?

This model is still a linear regression model. The structure of the model did not change. The model is still a linear combination of predictor variables related to the target variable. The predictor variables just do not all have a linear effect in terms of their relationship with \(y\). However, mathematically, it is still a linear combination and a linear regression model.

3.4.2 Global & Local Inference

In simple linear regression we could just look at the t-test for our slope parameter estimate to determine the utility of our model. With multiple parameter estimates comes multiple t-tests. Instead of looking at every individual parameter estimate initially, there is a way to determine the model adequacy for predicting the target variable overall.

The utility of a multiple regression model can be tested with a single test that encompasses all the coefficients from the model. This kind of test is called a global test since it tests all \(\beta\)’s simultaneously. The Global F-Test uses the F-distribution to do just that for multiple linear regression models. The hypotheses for this test are the following:

\[ H_0: \beta_1 = \beta_2 = \cdots = \beta_k = 0 \\ H_A: \text{at least one } \beta \text{ is nonzero} \]

In simpler terms, the null hypothesis is that none of the variables are useful in predicting the target variable. The alternative hypothesis is that at least one of these variables is useful in predicting the target variable.

The F-distribution is a distribution that has the following characteristics:

  • Bounded below by 0
  • Right-skewed
  • Both numerator and denominator degrees of freedom

A plot of a variety of F distributions is shown here:

## Warning: Removed 1500 rows containing missing values (`geom_line()`).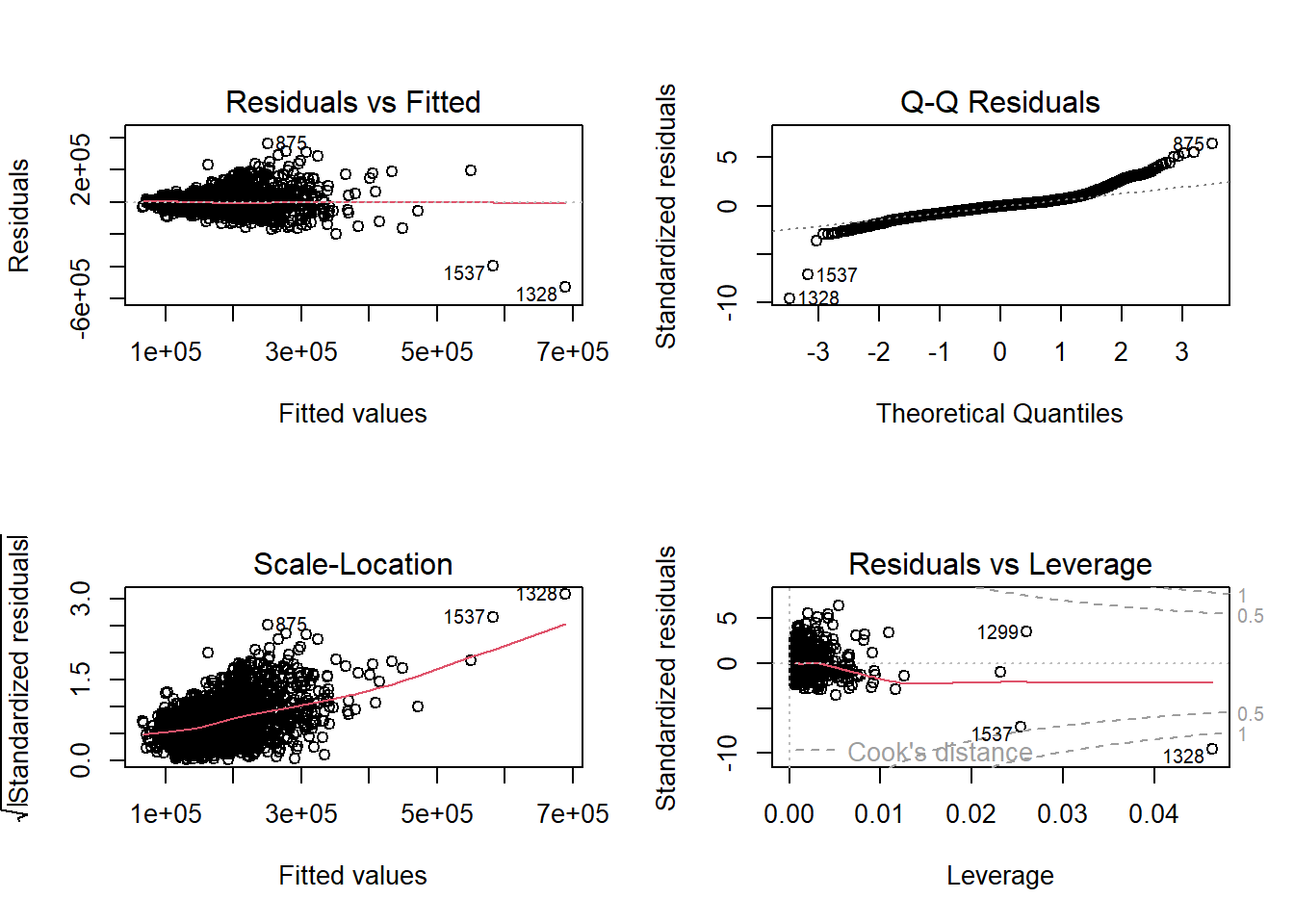

If the global test is significant, the next step would be to examine the individual t-tests to see which variables are significant and which ones are not. This is similar to post-hoc testing in ANOVA where we explored which of the categories was statistically different when we knew at least one was.

These tests are all available using the summary function on an lm function for linear regression. To build a multiple linear regression in R using the lm function, you just add another variable to the formula element. Here we will predict the sales price (Sale_Price) based on the square footage of the greater living area of the home (Gr_Liv_Area) as well as total number of rooms above ground (TotRms_AbvGrd).

ames_lm2 <- lm(Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd, data = train)

summary(ames_lm2)
## 
## Call:
## lm(formula = Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd, data = train)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -528656  -30077   -1230   21427  361465 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    42562.657   5365.721   7.932 3.51e-15 ***
## Gr_Liv_Area      136.982      4.207  32.558  < 2e-16 ***
## TotRms_AbvGrd -10563.324   1370.007  -7.710 1.94e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 56630 on 2048 degrees of freedom
## Multiple R-squared:  0.5024, Adjusted R-squared:  0.5019 
## F-statistic:  1034 on 2 and 2048 DF,  p-value: < 2.2e-16

At the bottom of the above output is the result of the global F-test. Since the p-value on this test is lower than the significance level of 0.05, we have statistical evidence that at least of the two variables - Gr_Liv_Area and TotRms_AbvGrd - is significant at predicting the sale price of the home. By looking at the individual t-tests in the output above, we can see that both variables are actually significant.

3.4.3 Assumptions

The main assumptions for the multiple linear regression model are the same as with the simple linear regression model:

  1. The expected value of \(y\) is linear in the \(x\)’s (proper model specification).
  2. The random errors are independent.
  3. The random errors are normally distributed.
  4. The random errors have equal variance (homoskedasticity).

However, with multiple variables there is an additional assumption that people tend to add to multiple linear regression modeling:

  1. No perfect collinearity (also called multicollinearity)

The new assumption means that no combination of predictor variables is a perfect linear combination with any other predictor variables. Collinearity, also called multicollinearity, occurs when predictor variables are correlated with each other. People often misstate this additional assumption as having no collinearity at all. This is too restrictive and basically impossible to meet in a realistic setting. Only when collinearity has a drastic impact on the linear regression do we need to concern ourselves. In fact, linear regression only completely breaks when that collinearity is perfect. Dealing with multicollinearity is discussed later.

Similar to simple linear regression, we can evaluate the assumptions by looking at residual plots. The plot function on the lm object provides these.

par(mfrow=c(2,2))
plot(ames_lm2)

par(mfrow=c(1,1))

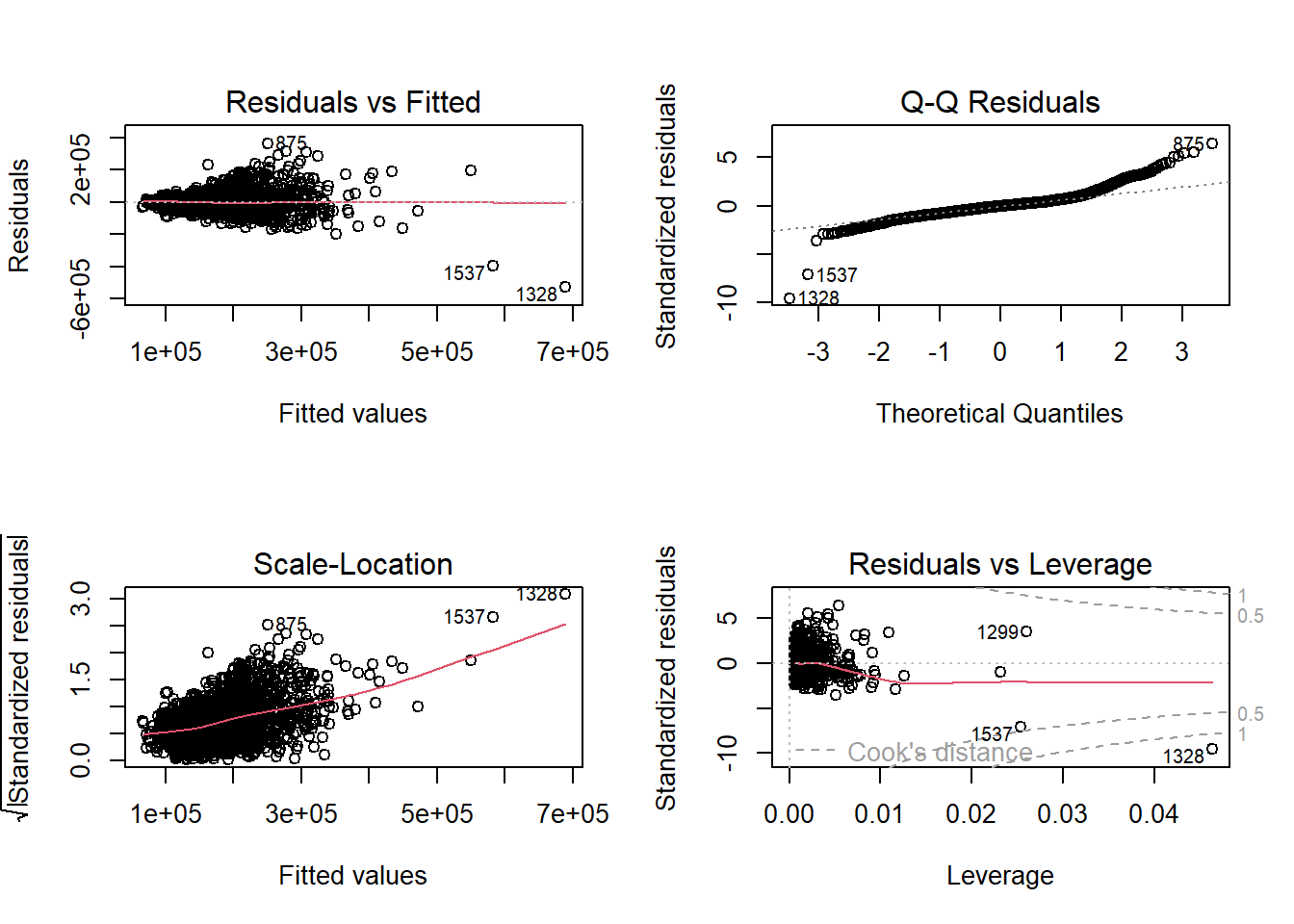
These will again be covered in much more detail in Diagnostic Chapter.

3.4.4 Multiple Coefficients of Determination

One of the main advantages of multiple linear regression is that the complexity of the model enables us to investigate the relationship among \(y\) and several predictor variables simultaneously. However, this increased complexity makes it more difficult to not only interpret the models, but also ascertain which model is “best.”

One example of this would be the coefficient of determination, \(R^2\), that we discussed earlier. The calculation for \(R^2\) is the exact same:

\[ R^2 = 1 - \frac{SSE}{TSS} \]

However, the problem with the calculation of \(R^2\) in a multiple linear regression is that the addition of any variable (useful or not) will never make the \(R^2\) decrease. In fact, it typically increases even with the addition of a useless variable. The reason is rather intuitive. When adding information to a regression model, your predictions can only get better, not worse. If a new predictor variable has no impact on the target variable, then the predictions can not get any worse than what they already were before the addition of the useless variable. Therefore, the \(SSE\) would never increase, making the \(R^2\) never decrease.

To account for this problem, there is the adjusted coefficient of determination, \(R^2_a\). The calculation is the following:

\[ R^2_a = 1 - [(\frac{n-1}{n-(k+1)})\times (\frac{SSE}{TSS})] \]

Notice what the calculation is doing. It takes the original ratio on the right hand side of the \(R^2\) equation, \(SSE/TSS\), and penalizes it. It multiplies this number by a ratio that is always greater than 1 if \(k > 0\). Remember, \(k\) is the number of variables in the model. Therefore, as the number of variables increases, the calculation penalizes the model more and more. However, if the reduction of SSE from adding a useful variable is low enough, then even with the additional penalization, the \(R^2_a\) will increase if the variable is a useful addition to the model. If the variable is not a useful addition to the model, the \(R^2_a\) will decrease. The \(R^2_a\) is only one of many ways to select the “best” model for multiple linear regression.

One downside of this new metric is that the \(R^2_a\) loses its interpretation. Since \(R^2_a \le R^2\), it is no longer bounded below by zero. Therefore, it can no longer be the proportion of variation explained in the target variable by the model. However, we can easily use \(R^2_a\) to select a model correctly and interpret that model with \(R^2\). Both of these numbers can be found using the summary function on the lm object from the previous model.

summary(ames_lm2)
## 
## Call:
## lm(formula = Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd, data = train)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -528656  -30077   -1230   21427  361465 
## 
## Coefficients:
##                 Estimate Std. Error t value Pr(>|t|)    
## (Intercept)    42562.657   5365.721   7.932 3.51e-15 ***
## Gr_Liv_Area      136.982      4.207  32.558  < 2e-16 ***
## TotRms_AbvGrd -10563.324   1370.007  -7.710 1.94e-14 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 56630 on 2048 degrees of freedom
## Multiple R-squared:  0.5024, Adjusted R-squared:  0.5019 
## F-statistic:  1034 on 2 and 2048 DF,  p-value: < 2.2e-16

From this output we can say that the combination of Gr_Liv_Area and TotRmsAbvGrd account for 50.24% of the variation in Sale_Price. Now let’s add a random variable to the model. This random variable will take random values from a normal distribution with mean of 0 and standard deviation of 1 and has no impact on the target variable.

set.seed(1234)
ames_lm3 <- lm(Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd + rnorm(length(Sale_Price), 0, 1), data = train)

summary(ames_lm3)
## 
## Call:
## lm(formula = Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd + rnorm(length(Sale_Price), 
##     0, 1), data = train)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -527926  -29943   -1298   21427  363925 
## 
## Coefficients:
##                                   Estimate Std. Error t value Pr(>|t|)    
## (Intercept)                      42589.091   5364.877   7.939 3.34e-15 ***
## Gr_Liv_Area                        136.927      4.207  32.548  < 2e-16 ***
## TotRms_AbvGrd                   -10552.425   1369.808  -7.704 2.05e-14 ***
## rnorm(length(Sale_Price), 0, 1)   1629.854   1259.478   1.294    0.196    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 56620 on 2047 degrees of freedom
## Multiple R-squared:  0.5028, Adjusted R-squared:  0.502 
## F-statistic: 689.9 on 3 and 2047 DF,  p-value: < 2.2e-16

Notice that the \(R^2\) of this model actually increased to 0.5028 from 0.5024. However, the \(R^2_a\) value stayed approximately the same at 0.502 since the addition of this new variable did not provide enough predictive power to outweigh the penalty of adding it.

3.4.5 Categorical Predictor Variables

As mentioned in EDA Section, there are two types of variables typically used in modeling:

  • Quantitative (or numeric)
  • Qualitative (or categorical)

Categorical variables need to be coded differently because they are not numerical in nature. As mentioned in EDA Section, two common coding techniques for linear regression are reference and effects coding. The interpretation of the coefficients (\(\beta\)’s) of these variables in a regression model depend on the specific coding used. The predictions from the model, however, will remain the same regardless of the specific coding that is used.

Let’s use the example of the Central_Air variable with 2 categories - Y and N. Using reference coding, the reference coded variable to describe these 2 categories (with N as the reference level) would be the following:

Central Air X1
Y 1
N 0
Table 3.1: Reference variable coding for the categorical attribute Central Air

The linear regression equation would be:

\[ \hat{y} = \hat{\beta}_0 + \hat{\beta}_1 X_1 \]

Let’s see the mathematical interpretation of the coefficient \(\hat{\beta}_1\). To do this, let’s get the average sale price of a home prediction for a home with central air (\(\hat{y}_Y\)) and without central air (\(\hat{y}_N\)):

\[ \hat{y}_Y = \hat{\beta}_0 + \hat{\beta}_1 \cdot 1 = \hat{\beta}_0 + \hat{\beta}_1 \\ \hat{y}_N = \hat{\beta}_0 + \hat{\beta}_1 \cdot 0 = \hat{\beta}_0 \]

By subtracting these two equations (\(\hat{y}_Y - \hat{y}_N = \hat{\beta}_1\)), we can get the prediction for the average difference in price between a home with central air and without central air. This shows that in reference coding, the coefficient on each dummy variable is the average difference between that category and the reference category (the category not represented with its own variable). The math can be extended to as many categories as needed.

Using effects coding, the effects coded variable to describe these 2 categories (with N as the reference level) would be the following:

Central Air X1
Y 1
N -1
Table 3.1: Effects variable coding for the categorical attribute Central Air

The linear regression equation would be:

\[ \hat{y} = \hat{\beta}_0 + \hat{\beta}_1 X_1 \]

Let’s see the mathematical interpretation of the coefficient \(\hat{\beta}_1\). To do this, let’s get the average sale price of a home prediction for a home with central air (\(\hat{y}_Y\)) and without central air (\(\hat{y}_N\)):

\[ \hat{y}_Y = \hat{\beta}_0 + \hat{\beta}_1 \cdot 1 = \hat{\beta}_0 + \hat{\beta}_1 \\ \hat{y}_N = \hat{\beta}_0 + \hat{\beta}_1 \cdot -1 = \hat{\beta}_0 - \hat{\beta}_1 \]

Similar to reference coding, the coefficient \(\hat{\beta}_1\) is the average difference between homes with central air and \(\hat{\beta}_0\). However, what is \(\hat{\beta}_0\)? By taking the average of our two predictions:

\[ \frac{1}{2} \times (\hat{y}_Y + \hat{y}_N) = \frac{1}{2} \times (\hat{\beta}_0 + \hat{\beta}_1 + \hat{\beta}_0 - \hat{\beta}_1) = \frac{1}{2} \times (2\hat{\beta}_0) = \hat{\beta}_0 \]

From this average we can get the prediction for the average difference in price between a home with central air and the average price across all homes. This shows that in effects coding, the coefficient on each dummy variable is the average difference between that category and the average price across all homes (including both with and without central air). The math can be extended to as many categories as needed.

Let’s see an example with Central_Air as a variable added to our multiple linear regression model as a reference coded variable.

ames_lm4 <- lm(Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd + Central_Air, data = train)

summary(ames_lm4)
## 
## Call:
## lm(formula = Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd + Central_Air, 
##     data = train)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -510745  -28984   -2317   20273  356742 
## 
## Coefficients:
##                Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   -7169.259   6778.879  -1.058     0.29    
## Gr_Liv_Area     129.594      4.131  31.374  < 2e-16 ***
## TotRms_AbvGrd -8980.938   1335.669  -6.724 2.29e-11 ***
## Central_AirY  54513.082   4762.926  11.445  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 54910 on 2047 degrees of freedom
## Multiple R-squared:  0.5323, Adjusted R-squared:  0.5316 
## F-statistic: 776.6 on 3 and 2047 DF,  p-value: < 2.2e-16

With these results we estimate the average difference in sales price between homes with central air and without central air to be $54,513.08.

3.4.6 Python Code

Global and Local Inference

model_mlr = smf.ols("Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd", data = train).fit()
model_mlr.summary()
OLS Regression Results
Dep. Variable: Sale_Price R-squared: 0.502
Model: OLS Adj. R-squared: 0.502
Method: Least Squares F-statistic: 1034.
Date: Tue, 18 Jun 2024 Prob (F-statistic): 4.37e-311
Time: 15:57:31 Log-Likelihood: -25355.
No. Observations: 2051 AIC: 5.072e+04
Df Residuals: 2048 BIC: 5.073e+04
Df Model: 2
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 4.256e+04 5365.721 7.932 0.000 3.2e+04 5.31e+04
Gr_Liv_Area 136.9821 4.207 32.558 0.000 128.731 145.233
TotRms_AbvGrd -1.056e+04 1370.007 -7.710 0.000 -1.33e+04 -7876.571
Omnibus: 408.938 Durbin-Watson: 2.020
Prob(Omnibus): 0.000 Jarque-Bera (JB): 6517.477
Skew: 0.473 Prob(JB): 0.00
Kurtosis: 11.682 Cond. No. 6.86e+03


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.86e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

Assumptions

train['pred_mlr'] = model_mlr.predict()
train['resid_mlr'] = model_mlr.resid

train[['Sale_Price', 'pred_mlr', 'resid_mlr']].head(n = 10)
##    Sale_Price       pred_mlr     resid_mlr
## 0      232600  172585.780285  60014.219715
## 1      166000  209070.126180 -43070.126180
## 2      170000  198749.366853 -28749.366853
## 3      252000  215018.840374  36981.159626
## 4      134000  144809.807959 -10809.807959
## 5      164700  160973.699138   3726.300862
## 6      193500  198612.384724  -5112.384724
## 7      118500  145752.982966 -27252.982966
## 8       94000  109742.383030 -15742.383030
## 9      111250  108098.597486   3151.402514
sm.qqplot(train['resid_mlr'])
plt.show()

Multiple Coefficient of Determination

model_mlr.summary()
OLS Regression Results
Dep. Variable: Sale_Price R-squared: 0.502
Model: OLS Adj. R-squared: 0.502
Method: Least Squares F-statistic: 1034.
Date: Tue, 18 Jun 2024 Prob (F-statistic): 4.37e-311
Time: 15:57:32 Log-Likelihood: -25355.
No. Observations: 2051 AIC: 5.072e+04
Df Residuals: 2048 BIC: 5.073e+04
Df Model: 2
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept 4.256e+04 5365.721 7.932 0.000 3.2e+04 5.31e+04
Gr_Liv_Area 136.9821 4.207 32.558 0.000 128.731 145.233
TotRms_AbvGrd -1.056e+04 1370.007 -7.710 0.000 -1.33e+04 -7876.571
Omnibus: 408.938 Durbin-Watson: 2.020
Prob(Omnibus): 0.000 Jarque-Bera (JB): 6517.477
Skew: 0.473 Prob(JB): 0.00
Kurtosis: 11.682 Cond. No. 6.86e+03


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 6.86e+03. This might indicate that there are
strong multicollinearity or other numerical problems.

Categorical Predictor Variables

model_mlr2 = smf.ols("Sale_Price ~ Gr_Liv_Area + TotRms_AbvGrd + C(Central_Air)", data = train).fit()
model_mlr2.summary()
OLS Regression Results
Dep. Variable: Sale_Price R-squared: 0.532
Model: OLS Adj. R-squared: 0.532
Method: Least Squares F-statistic: 776.6
Date: Tue, 18 Jun 2024 Prob (F-statistic): 0.00
Time: 15:57:32 Log-Likelihood: -25292.
No. Observations: 2051 AIC: 5.059e+04
Df Residuals: 2047 BIC: 5.061e+04
Df Model: 3
Covariance Type: nonrobust
coef std err t P>|t| [0.025 0.975]
Intercept -7169.2593 6778.879 -1.058 0.290 -2.05e+04 6124.960
C(Central_Air)[T.Y] 5.451e+04 4762.926 11.445 0.000 4.52e+04 6.39e+04
Gr_Liv_Area 129.5945 4.131 31.374 0.000 121.494 137.695
TotRms_AbvGrd -8980.9382 1335.669 -6.724 0.000 -1.16e+04 -6361.527
Omnibus: 463.227 Durbin-Watson: 2.032
Prob(Omnibus): 0.000 Jarque-Bera (JB): 7273.636
Skew: 0.621 Prob(JB): 0.00
Kurtosis: 12.142 Cond. No. 9.92e+03


Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 9.92e+03. This might indicate that there are
strong multicollinearity or other numerical problems.